Simulating Cost Flow
This post assumes knowledge of min/max cost flow and a rough understanding of the high-level methods for solving (successive shortest path and cycle canceling). Knowledge of specific algorithms and implementation details are not expected. Also solutions to some problems will use Aliens trick.
The cost flow problem is a well-known problem in literature that a whole slew of competitive programming problems can be formulated as. Unfortunately, competitive programming problems typically have constraints set too high for directly running even the most state of the art cost flow algorithm. However, in certain problems the flow network will have a very specific setup that allows us to figure out greedily the optimal flow (i.e. proving greedy with flow) or “simulate” the flow algorithm faster with data structures. That is what this post will be about.
I will say that I do not claim novelty over these ideas. This idea is (unsurprisingly) well-known in China. This particular post and some of the example problems are taken from this Chinese blog.
I will also describe everything below in terms of min cost flow, max cost is of course analogous. When describing flow network constructions, I will shorthand with $(cost, capacity)$ for describing edges.
High-level Methods for Cost Flow
Most cost flow algorithms fall into one of these categories of high-level approaches. The two in particular that we will look at are:
- Successive Shortest Path: Repeatedly find a min cost augmenting path (a path with minimum total cost where all edges can still contain more flow) from source to sink and send flow through that path.
- Cycle Cancelling: Repeatedly find a negative cost cycle (a cycle with negative total cost where all edges can still contain more flow) and send flow through that cycle.
Note that in the cycle cancelling paradigm, there is no concept of source and sink, but you can solve for source and sink by adding an edge from sink to source with cost of $-\infty$ and capacity of $k$ for the min cost $k$-flow (or $\infty$ capacity if you want min cost max flow).
Min Cost Flow is Convex
Min cost flow as a function of amount of flow is convex. This makes intuitive sense, as you can always rearrange the augmenting paths you choose to pick less steep ones (lower cost) before more steep ones (higher cost). This fact is useful as it allows us to use Aliens trick.
Codeforces 802O: April Fools’ Problem
Statement Summary: You are preparing and printing $k$ problems for a contest over the course of $n$ days. On the $i$th day, you can prepare a problem for cost $a_i$ and print a problem for cost $b_i$. You must prepare a problem before printing it. In other words, if you prepare a problem on day $i$, you can only print it on some day $j \geq i$. You can prepare and print at most one problem per day. What is the minimum cost of preparing and printing $k$ problems?
Constraints: $1 \leq k \leq n \leq 5 \cdot 10^5, 1 \leq a_i, b_i \leq 10^9$
Let’s first think about solving this with flows. One straightforward way is to create $2n + 2$ nodes: a source $s$ and sink $t$, plus nodes representing $a_i$ and $b_i$ for each $i$. We add the following edges:
- $s$ to each $a_i$ node with $(a_i, 1)$
- each $b_i$ node to $t$ with $(b_i, 1)$
- each $a_i$ node to $b_j$ node where $i \leq j$ with $(0, 1)$
The answer is the min cost $k$-flow of this network.
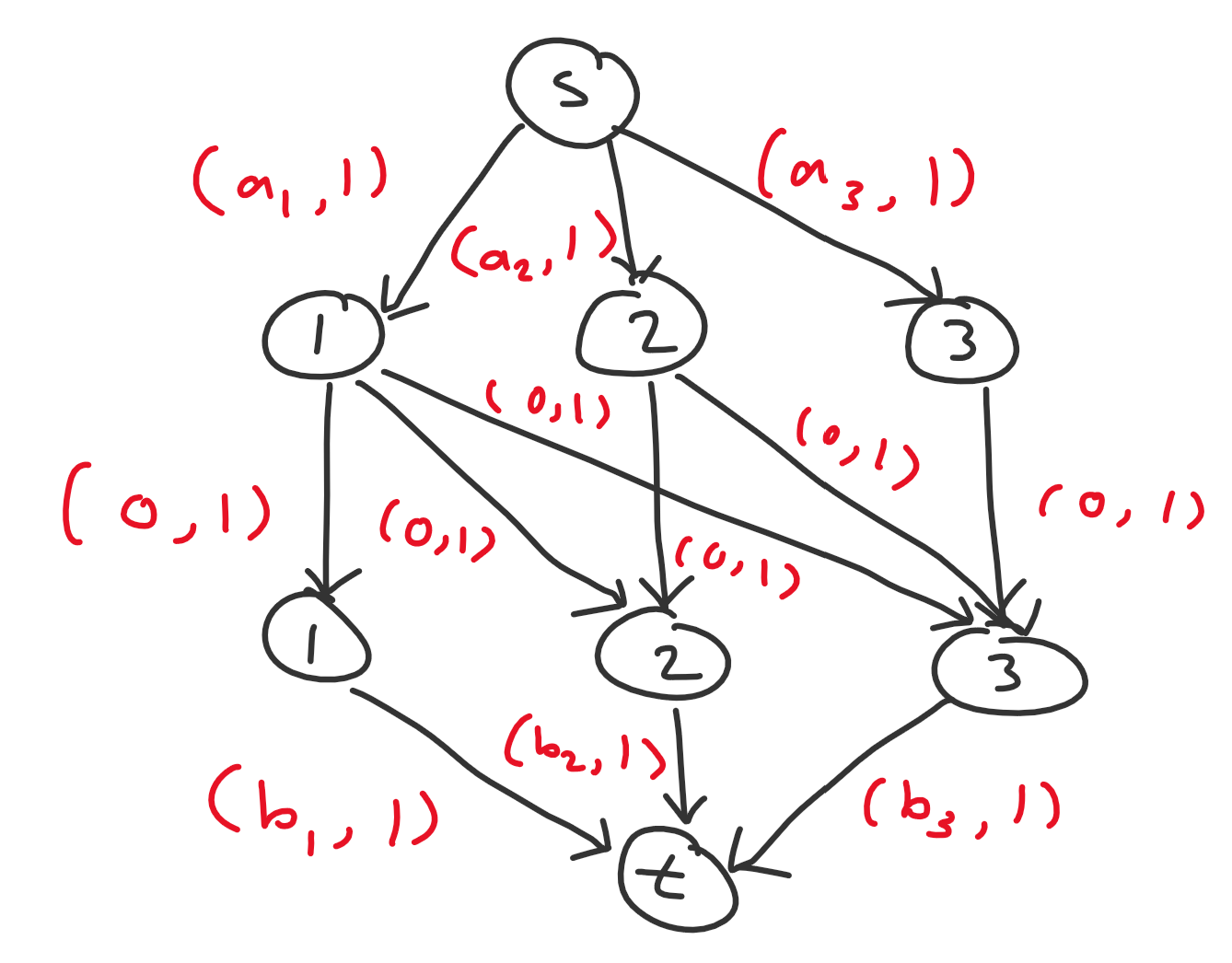
Example for $n = 3$
Now let’s try to optimize using one of two methods. Both are possible and lead to different solutions for this problem.
Successive Shortest Path
This is the method described in the official editorial.
First, let’s simplify this network to not use $\Omega(n^2)$ edges. Consider a slightly different setup with $n + 2$ nodes: a source $s$ and sink $t$, plus nodes $1$ through $n$. We add the following edges:
- $s$ to each $i$ with $(a_i, 1)$
- each $i$ to $t$ with $(b_i, 1)$
- $i$ to $i + 1$ with $(0, \infty)$
I claim the answer is also the min cost $k$-flow of this network. Essentially, a matching consists of picking some $a_i$, waiting zero or more days (represent by taking some number of $i \to i + 1$ edges), and then pick some $b_j$ where $i \leq j$.
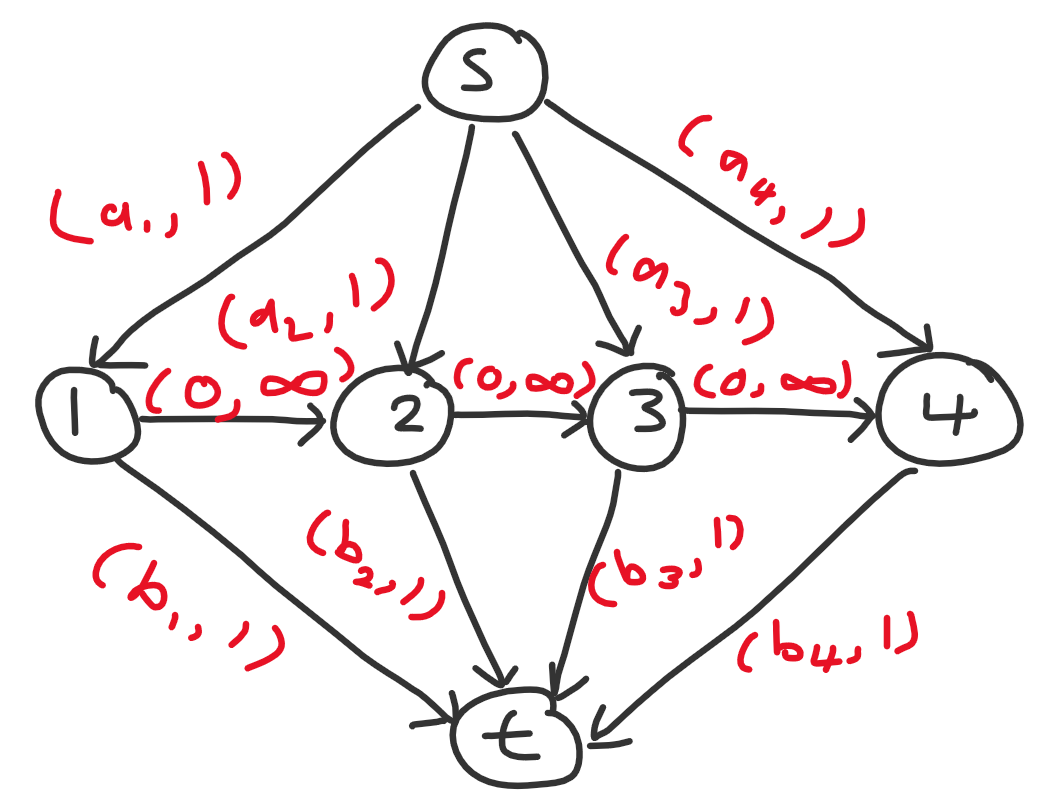
Example for $n = 4$
An augmenting path consists of sending flow from $s$ to some $i$, then from $i$ to $j$, and finally from $j$ to $t$.
- $s \to i$ and $j \to t$ must of course have no flow going through them.
- If $i \leq j$, this is ok. We add $+1$ flow to each edge on the path from $i$ to $j$.
- If $i > j$, then we are sending flow along a reverse edge and cancelling out existing flow, so every edge on the path from $i$ to $j$ must have at least $1$ flow, and the augmenting path adds $-1$ flow to each path edge.
And in the successive shortest path algorithm, we simply need to choose the augmenting path with minimum cost each time. So we need to choose a pair of indices $i, j$ with minimum $a_i + b_j$, and either $i \leq j$ or there exists flow on every edge on the path between $i$ and $j$.
So we need to be able to add $+1$ or $-1$ to a range and recompute the minimum cost valid $(i, j)$ pair. This sounds like a job for lazy segment tree! We just repeat $k$ times of querying the segtree for $(i, j)$ and either add $+1$ or $-1$ to all edges in between $i$ and $j$, giving us an $\mathcal O(k \log n)$ solution.
The details for determining the minimum cost valid $(i, j)$ pair are quite tedious, but the TLDR is that you have to store first and second minimums of the amount of flow through any edge in a subarray. I have an old submission that implements this idea with a ton of variables in the segtree node. It can probably be reduced with more thought.
Cycle Cancelling
To drastically simplify our analysis, we will apply Aliens trick. Binary search on some reward $c$, so now there is no requirement of at least $k$ problems anymore, but instead you get a reward of $c$ for completing one problem. So preparing a problem on day $i$ and printing on day $j$ costs $a_i + b_j - c$. So there is an edge from $t$ to $s$ with $(-c, \infty)$. We binary search for the minimum $c$ that we complete at least $k$ problems. This is valid because we know min cost flow is convex with respect to the amount of flow.
Now consider incrementally adding in nodes in decreasing order (from $n$ to $1$) and consider how the optimal flow changes after each additional node. When we add node $i$, we add edges $s \to a_i$, $b_i \to t$, and $a_i \to b_j$ for all $i \leq j$. Upon adding node $i$, we consider the possibilities for how a new negative cycle could form.
- $s \to a_i \to b_j \to t \to s$ with cost $a_i + b_j - c$. This is essentially matching $a_i$ with some unmatched $b_j$.
- $s \to a_i \to b_j \to a_k \to s$ with cost $a_i - a_k$. This is cancelling out some existing flow passing through $s \to a_k \to b_j$ and is equivalent to changing the matching to match $b_j$ with $a_i$ instead of $a_k$.
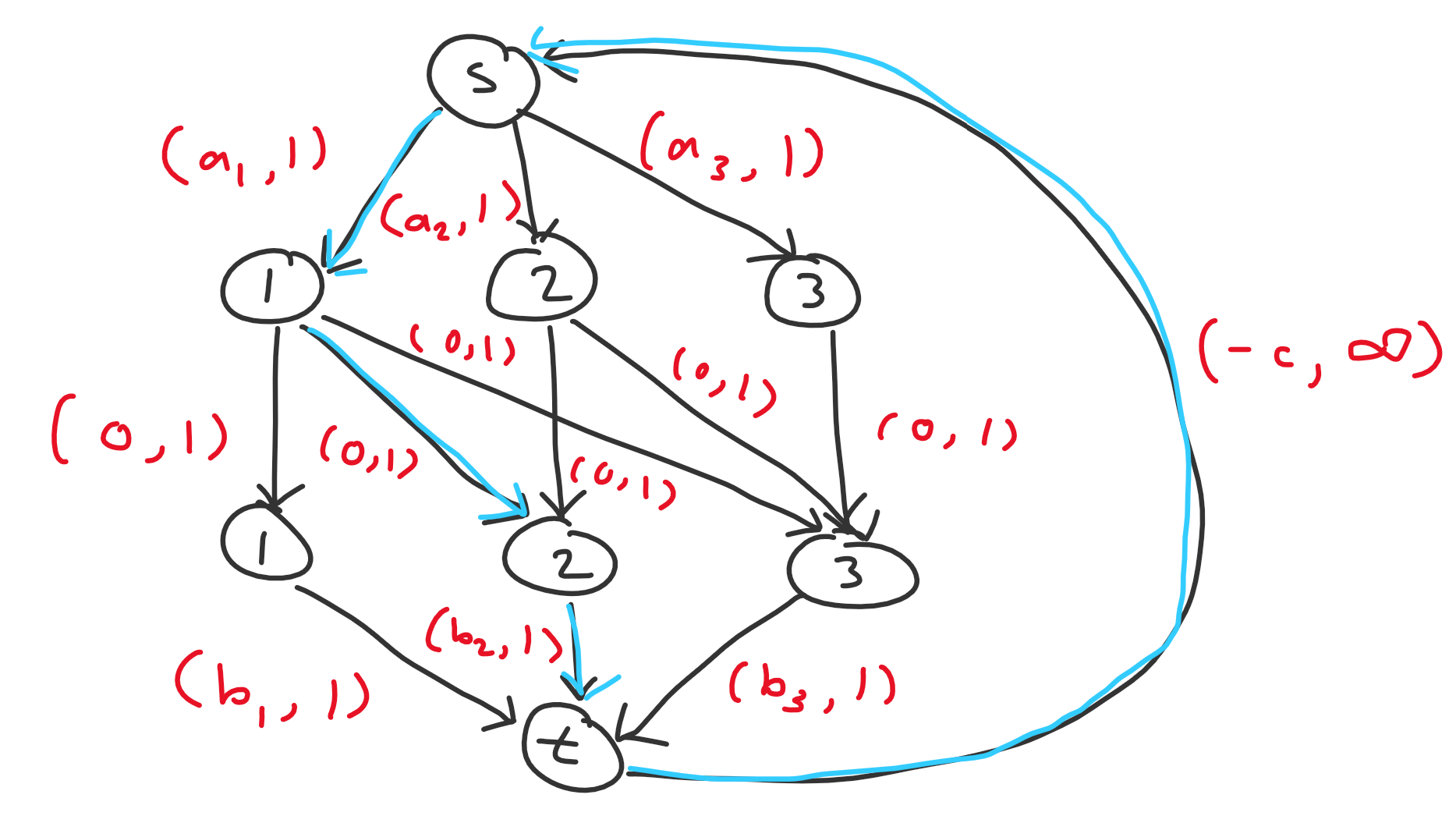
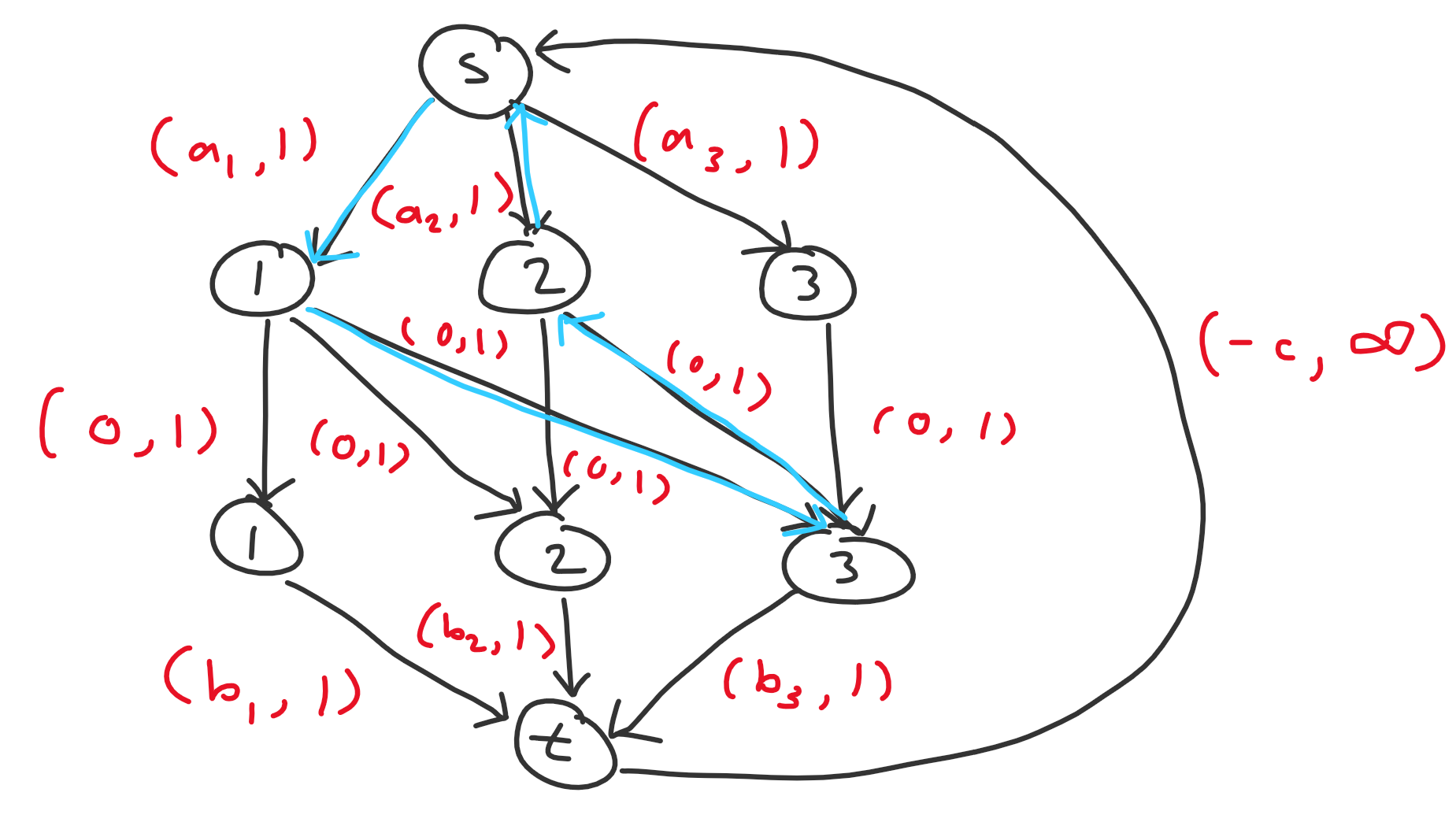
Examples of negative cycles of the first and second types
Those are actually the only two cases we need to consider. For example, you might think we need to consider some cycle of the form $s \to a_i \to b_j \to t \to b_k \to a_l \to s$. This cycle would represent taking some matched pair $(a_i, b_j)$ instead of $(a_l, b_k)$. However, if $(a_l, b_k)$ was originally matched in the first place, that would imply $a_l + b_k \leq c$, as otherwise $t \to b_j \to a_i \to s \to t$ would be a negative cycle with weight $c - a_l - b_k$ and we would have had to handle that before adding node $i$. And if $s \to a_i \to b_j \to t \to b_k \to a_l \to s$ was a negative cycle, that would imply $a_i + b_j < a_l + b_k$ and therefore $a_i + b_j < c$, so we could instead take the negative cycle $s \to a_i \to b_j \to t \to s$. In fact, we would ultimately converge to that state regardless, because if we took $s \to a_i \to b_j \to t \to b_k \to a_l \to s$ first, then $s \to a_l \to b_k \to t \to s$ would form a negative cycle afterwards, so the end result after resolving all negative cycles is identical.
You can also confirm that after taking a negative cycle of one of the two types listed above (whichever one is more negative), we will not create any more additional negative cycles. So essentially, each time we add a node $i$ to the network, we take at most one additional negative cycle.
Example: Can taking a type 2 cycle lead to creating a type 1 cycle?
If we break up some old pair $(a_k, b_j)$ and instead match $(a_i, b_j)$, is it then possible for $a_k$ to be paired with some other $b_l$?
If we are breaking up the pair, that implies $a_i < a_k$. Now suppose we pair $a_k$ with $b_l$, implying $a_k + b_l < c$. Substituting $a_i < a_k$ yields $a_i + b_l < c$. Furthermore, if we compare $a_i - a_k$ and $a_i + b_l - c$, because $-a_k > b_l - c$, $a_i + b_l - c < a_i - a_k$, so it is more optimal to match $a_i$ with $b_l$ in the first place.
Therefore, we can simply maintain a priority queue of potential negative cycles and iterate $i$ from $n$ to $1$. When we match $(a_i, b_j)$, we insert $-a_i$ into the priority queue to allow for breaking up that matching and pairing $b_j$ with something else in the future. When we leave $b_i$ unmatched, we insert $b_i - c$ into the priority queue to allow for matching with that $b_i$ in the future. And at each step, if $a_i$ plus the minimum value in the priority queue is less than $0$, then we take that option. The overall complexity is $\mathcal O(n \log n \log A)$ (but with much better constant than the successive shortest path solution).
Code for Clarity
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
auto solve = [&] (int c) -> pair<int, long long> {
int cnt = 0;
long long cost = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
for (int i=n-1; i>=0; i--) {
pq.emplace(b[i] - c, 0);
if (a[i] + pq.top().first <= 0) {
cnt += pq.top().second == 0;
cost += a[i] + pq.top().first;
pq.pop();
pq.emplace(-a[i], 1);
}
}
return {cnt, cost + (long long) k * c};
};
int l = 0, r = 2e9 + 5;
while (l < r) {
int m = midpoint(l, r);
if (solve(m).first >= k)
r = m;
else
l = m + 1;
}
cout << solve(l).second << "\n";
The priority queue stores negative cycles as a pair of cost and what type it is (swapping with existing matching or creating a new matching). Note that solve tries to maximize the number of matchings created for tiebreakers, which is necessary to avoid reconstruction issues with Aliens trick (touched on in more detail in the Aliens trick resource I linked at the top).
Notice that the final solution looks awfully similar to a greedy algorithm. And indeed, we can apply a greedy interpretation to this: each $a_i$ can be matched with some $b_j$ where $i \leq j$ for cost $a_i + b_j - c$, and we want cost as negative as possible. Then the two types of negative cycles can be interpreted as “options” when introducing a new index $i$: either match $a_i$ with some unmatched $b_j$ or swap it with some existing $(a_k, b_l)$ matching. In essence, the flow interpretation serves as a proof for the correctness of the greedy.
Do we need Aliens trick?
Maybe not, but the solution certainly gets significantly messier without it. If we don’t apply Aliens trick and instead analyze the network directly, we have an edge from $t$ to $s$ with $(-\infty, k)$.
For types of negative cycles introduced upon adding a new index $i$, the two types described above still apply, but now $s \to a_i \to b_j \to t \to b_k \to a_l \to s$ is also possible, because the $t \to s$ edge no longer has infinite capacity, so it may not be possible to choose $s \to a_i \to b_j \to t \to s$ instead.
Furthermore, not only is $s \to a_i \to b_j \to t \to b_k \to a_l \to s$ possible, but there are even more complicated types of cycles that could spawn now. Consider the following case:
1
2
3
5 3
9 1 10 10 4
6 7 8 2 9
After processing $i = 5, 4, 3$, our matchings will be $(10, 8), (10, 2), (4, 9)$ for total cost of $43$.
When we introduce $i = 2$, we can no longer take any more matchings as $k = 3$, so we will have to consider swapping with existing matchings instead. The most negative cycle available is swapping out $(1, 7)$ for $(10, 8)$ for cost $1 + 7 - 10 - 8 = -10$. This is a negative cycle of the third type that didn’t exist with Aliens trick, namely $s \to a_2 \to b_2 \to t \to b_3 \to a_3 \to s$. And so now we have $(1, 7), (10, 2), (4, 9)$ with total cost $33$.
Now introduce $i = 1$. The most negative cycle is $s \to a_1 \to b_4 \to a_4 \to s$ with cost $9 - 10 = -1$. So after swapping, we have matchings $(9, 2), (1, 7), (4, 9)$. However, we are not done. There’s still a long negative cycle that exists in this situation: $t \to b_2 \to a_2 \to b_4 \to a_1 \to b_1 \to t$ with cost $-7 + 6 = -1$. What this does is this matches the $9$ with the $6$ instead and then matches the $1$ with the $2$ instead of the $7$. So this converges to $(9, 6), (1, 2), (4, 9)$ with the minimum cost of $31$.
If we were to do this in one negative cycle after adding $i = 1$, it would be $s \to a_1 \to b_1 \to t \to b_2 \to a_2 \to b_4 \to a_4 \to s$ with cost $9 + 6 - 7 - 10 = -2$. That’s absurd!
In short, when there is a capacity $k$ restriction, it is no longer the case that the optimal solution containing $i$ from $2$ to $n$ changes just a little bit when adding $i = 1$. It could completely morph.
So with this first example, we can see two different solutions that arise from thinking about flows. The first one is probably impossible to think of without flows. For the second one, it might be difficult to prove Aliens trick can be applied here without formulating it as flow. Once Aliens trick is applied, the greedy is relatively easier to come up without thinking about flows, but having the flow network still gives us confidence in its correctness.
Codeforces 866D: Buy Low Sell High
Statement Summary: You have knowledge of the price of a stock over the next $n$ days. On the $i$th day it will have price $p_i$. On each day you can either buy one share of the stock, sell one existing share you currently have, or do nothing. You cannot sell shares you do not have. What is the maximum possible profit you can earn?
Constraints: $2 \leq n \leq 3 \cdot 10^5, 1 \leq p_i \leq 10^6$
This problem has several interpretations that lead to the same code. You can think of it as slope trick. Or as greedy. Let’s think about it as flows.
Firstly, we can loosen the restrictions by allowing for both buying and selling a stock on a given day. This won’t change the answer since both buying and selling on the same day is equivalent to doing nothing.
Now we design the following flow network with $n + 2$ nodes: a source $s$ and sink $t$ and $n$ nodes representing days $1$ through $n$. We add the following edges:
- $s$ to $i$ for all $1 \leq i \leq n$ with $(-p_i, 1)$
- $i$ to $t$ for all $1 \leq i \leq n$ with $(p_i, 1)$
- $i$ to $i + 1$ for all $1 \leq i < n$ with $(0, \infty)$
The answer is thus the max cost flow of this network.
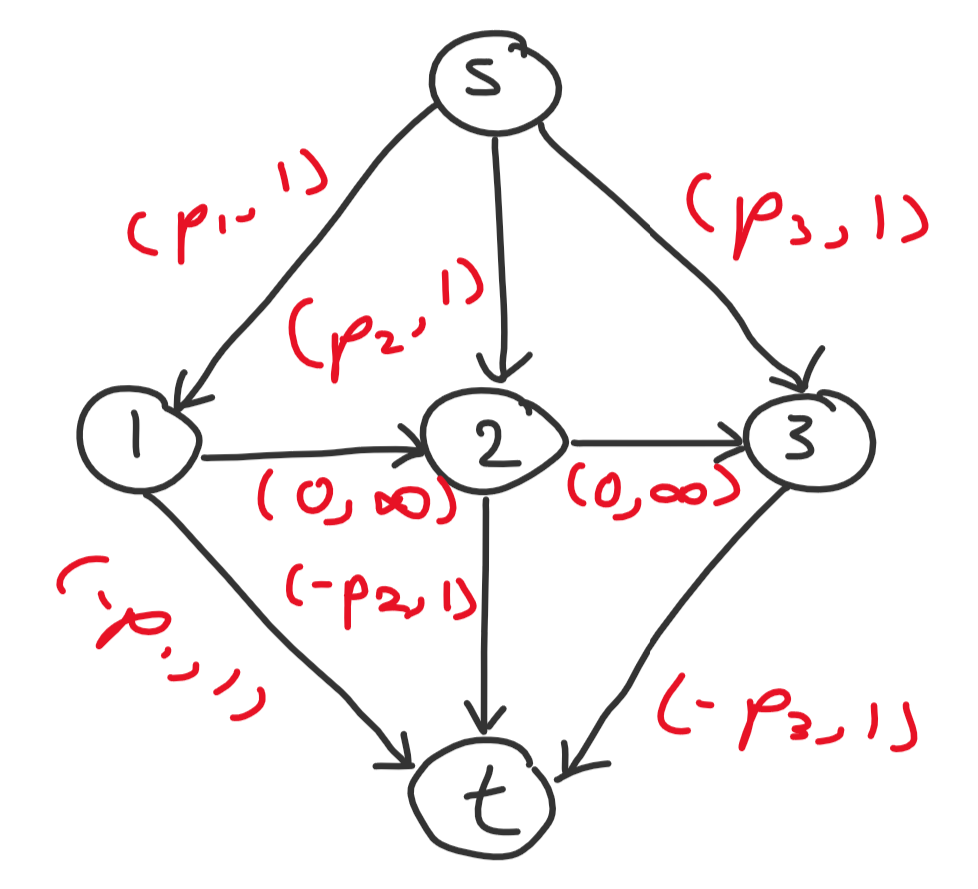
Example for $n = 3$
Now consider the cycle cancelling method. Add an edge from $t$ to $s$ with $(0, \infty)$. We are using a cost of $0$ instead of $\infty$ because we do not require the max amount of flow, and forcing the max flow is not always optimal.
This network is extremely similar to the previous problem. We add the nodes from $n$ to $1$. When we add node $i$, the possible positive (since we are doing max cost flow) cycles are:
- $s \to i \to \dots \to j \to t \to s$ for $i \leq j$ with cost $p_j - p_i$
- $s \to i \to \dots \to j \to s$ for $i \leq j$ also with cost $p_j - p_i$
So the code ends up being quite simple and may resemble some other greedy code you’ve seen.
Code
1
2
3
4
5
6
7
8
9
10
long long ret = 0;
priority_queue<int> pq;
for (int i=n-1; i>=0; i--) {
pq.push(p[i]);
if (pq.top() > p[i]) {
ret += pq.top() - p[i];
pq.pop();
pq.push(p[i]);
}
}
CSES Programmers and Artists
Statement Summary: You have $n$ people, the $i$th person has $x_i$ amount of programming skill and $y_i$ amount of art skill. Each person can be assigned to be a programmer, artist, or neither. You need exactly $a$ programmers and $b$ artists. What is the maximum sum of skills attainable by some matching?
Constraints: $1 \leq n \leq 2 \cdot 10^5, a + b \leq n, 1 \leq x_i, y_i \leq 10^9$
You get the drill now. Let’s model this problem as a flow network. Here is one possible construction using $n + 4$ nodes.
- $s$ to $i$ with $(0, 1)$
- $i$ to $prog$ with $(x_i, 1)$
- $i$ to $art$ with $(y_i, 1)$
- $prog$ to $t$ with $(0, a)$
- $art$ to $t$ with $(0, b)$
The answer is the max cost max flow of this network. Notice that in this case the maximum flow is also optimal as all augmenting paths will have positive weight.
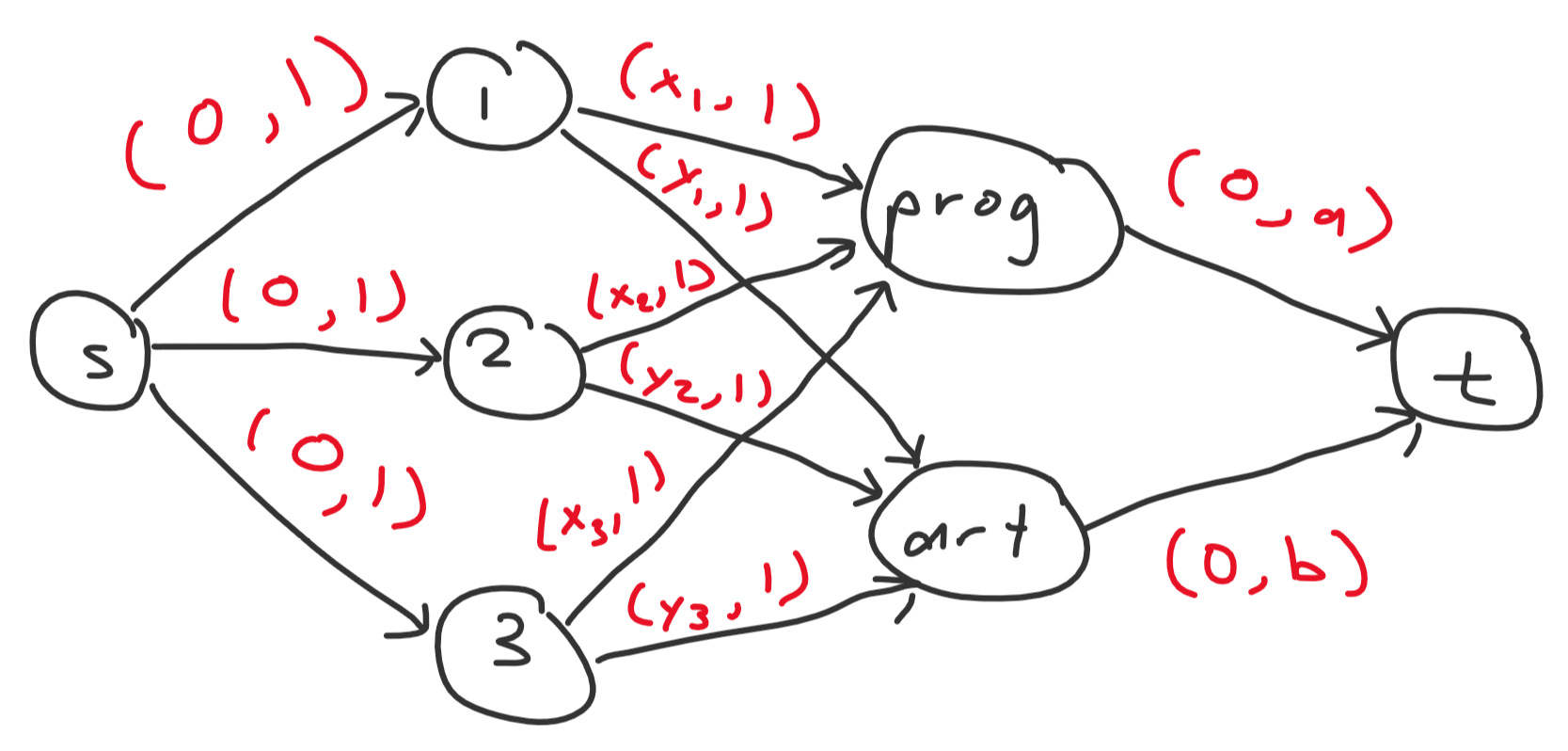
Example for $n = 3$
Let’s try approaching this with successive shortest path! Essentially, we repeatedly find an augmenting path from $s$ to $t$ with maximum cost and send $1$ unit of flow through. After some pondering, we conclude we only have $4$ types of paths to consider.
- $s \to i \to prog \to t$ with cost $x_i$
- $s \to i \to art \to t$ with cost $y_i$
- $s \to i \to prog \to j \to art \to t$ with cost $x_i - x_j + y_j$
- $s \to i \to art \to j \to prog \to t$ with cost $y_i - y_j + x_j$
The first and fourth types of paths decrease the capacity of $prog \to t$ by $1$, and the second and third types of paths decrease the capacity of $art \to t$ by $1$.
Do we need to consider any more complicated paths? Such as $s \to i \to prog \to j \to art \to k \to prog \to t$? Turns out we don’t. Suppose path $s \to i \to prog \to j \to art \to k \to prog \to t$ has the maximum cost. The cost is $x_i - x_j + y_j - y_k + x_k$. Now consider a different augmenting path that would also be valid, $s \to i \to prog \to t$ with cost $x_i$. The fact that the other path was chosen implies $x_i - x_j + y_j - y_k + x_k > x_i$, or $y_j - x_j + x_k - y_k > 0$. This implies that there exists a positive cycle $j \to art \to k \to prog \to j$ before introducing our new augmenting path, contradicting the property of successive shortest paths which ensures optimal cost flow with each new augmenting path added.
Therefore, we just need to maintain some heaps to repeatedly find the maximum cost path out of those $4$ options:
- pair unmatched $i$ to programmer
- pair unmatched $i$ to artist
- pair unmatched $i$ to programmer, and switch some existing programmer $j$ to artist
- pair unmatched $i$ to artist, and switch some existing artist $j$ to programmer
My code is a bit verbose but attempts to implement this idea as straightforwardly as possible:
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define DEBUG(...) debug(#__VA_ARGS__, __VA_ARGS__)
#else
#define DEBUG(...) 6
#endif
template<typename T, typename S> ostream& operator << (ostream &os, const pair<T, S> &p) {return os << "(" << p.first << ", " << p.second << ")";}
template<typename C, typename T = decay<decltype(*begin(declval<C>()))>, typename enable_if<!is_same<C, string>::value>::type* = nullptr>
ostream& operator << (ostream &os, const C &c) {bool f = true; os << "["; for (const auto &x : c) {if (!f) os << ", "; f = false; os << x;} return os << "]";}
template<typename T> void debug(string s, T x) {cerr << "\033[1;35m" << s << "\033[0;32m = \033[33m" << x << "\033[0m\n";}
template<typename T, typename... Args> void debug(string s, T x, Args... args) {for (int i=0, b=0; i<(int)s.size(); i++) if (s[i] == '(' || s[i] == '{') b++; else
if (s[i] == ')' || s[i] == '}') b--; else if (s[i] == ',' && b == 0) {cerr << "\033[1;35m" << s.substr(0, i) << "\033[0;32m = \033[33m" << x << "\033[31m | "; debug(s.substr(s.find_first_not_of(' ', i + 1)), args...); break;}}
template<typename T>
struct FastSet {
priority_queue<T> pq, pending;
void add(T x) {
pq.push(x);
}
void rem(T x) {
pending.push(x);
while (!pq.empty() && !pending.empty() && pq.top() == pending.top()) {
pq.pop();
pending.pop();
}
}
T max() {
assert(!pq.empty());
return pq.top();
}
};
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int a, b, n;
cin >> a >> b >> n;
vector<int> x(n), y(n);
for (int i=0; i<n; i++)
cin >> x[i] >> y[i];
FastSet<pair<int, int>> pqA, pqB;
priority_queue<pair<int, int>> pqA2, pqB2;
for (int i=0; i<n; i++) {
pqA.add({x[i], i});
pqB.add({y[i], i});
}
long long ret = 0;
while (a > 0 || b > 0) {
int mx = 0;
if (a > 0) {
if (!pqA.pq.empty())
mx = max(mx, pqA.max().first);
if (!pqB.pq.empty() && !pqB2.empty())
mx = max(mx, pqB.max().first + pqB2.top().first);
}
if (b > 0) {
if (!pqB.pq.empty())
mx = max(mx, pqB.max().first);
if (!pqA.pq.empty() && !pqA2.empty())
mx = max(mx, pqA.max().first + pqA2.top().first);
}
assert(mx > 0);
ret += mx;
if (a > 0) {
if (!pqA.pq.empty() && mx == pqA.max().first) {
int i = pqA.max().second;
pqA.rem({x[i], i});
pqB.rem({y[i], i});
pqA2.emplace(y[i] - x[i], i);
a--;
continue;
}
if (!pqB.pq.empty() && !pqB2.empty() && mx == pqB.max().first + pqB2.top().first) {
int i = pqB.max().second, j = pqB2.top().second;
pqA.rem({x[i], i});
pqB.rem({y[i], i});
pqB2.pop();
pqB2.emplace(x[i] - y[i], i);
pqA2.emplace(y[j] - x[j], j);
a--;
continue;
}
}
if (b > 0) {
if (!pqB.pq.empty() && mx == pqB.max().first) {
int i = pqB.max().second;
pqA.rem({x[i], i});
pqB.rem({y[i], i});
pqB2.emplace(x[i] - y[i], i);
b--;
continue;
}
if (!pqA.pq.empty() && !pqA2.empty() && mx == pqA.max().first + pqA2.top().first) {
int i = pqA.max().second, j = pqA2.top().second;
pqA.rem({x[i], i});
pqB.rem({y[i], i});
pqA2.pop();
pqA2.emplace(y[i] - x[i], i);
pqB2.emplace(x[j] - y[j], j);
b--;
continue;
}
}
assert(false);
}
cout << ret << "\n";
return 0;
}
More Problems
- Codeforces 280D: k-Maximum Subsequence Sum
- NOI 2019: Sequence
- CCPC Finals 2021 Problem I: Reverse LIS
- Any other example problem from this blog
 Subscribe to receive notifications when a new post drops
Subscribe to receive notifications when a new post drops